Qual è un buon clustering?¶
Innanzitutto dovremmo rispondere alla domanda: cos'è un cluster?...non è facile rispondere a questa domanda...
- Sicuramente un buon clustering rispetta due criteri fondamentali:
- Coesione interna: Alta similarità tra gli oggetti della staessa classe.
- Dissimilarità esterna: Bassa similarità tra oggetti di classi differenti.
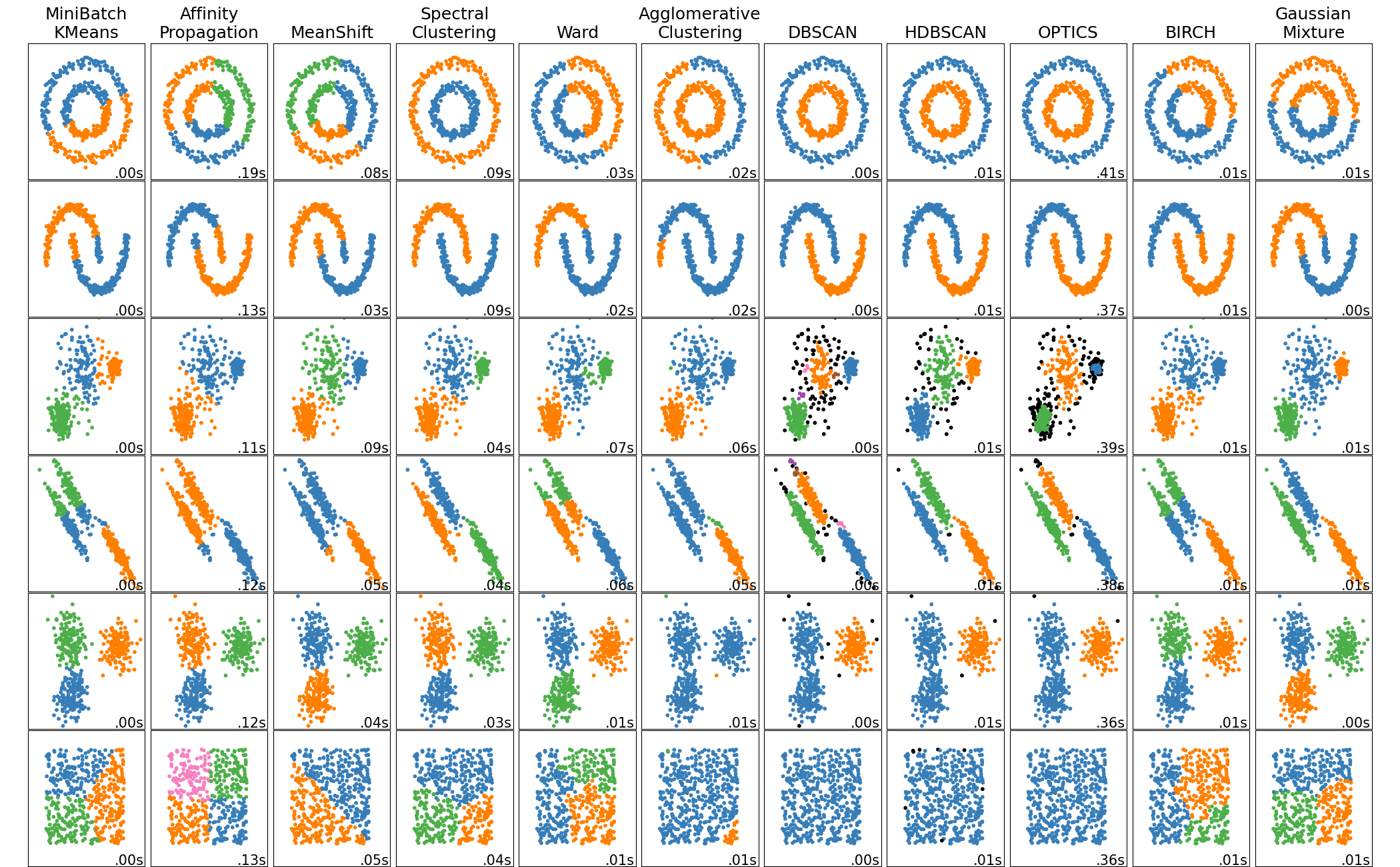
Approcci che vedremo¶
- Approccio di tipo Partitioning:
- Construct various partitions and then evaluate them by some criterion, e.g., minimizing the sum of square errors.
- Caso di studio: K-Means
- Approccio di tipo Density-based:
- Based on connectivity and density functions.
- Caso di studio: DBSCAN
K-Means¶
Algoritmo¶
Supponiamo di avere $\{\mathbf{x}_{1}, \dots, \mathbf{x}_{n}\}$ osservazioni di una variabile $\mathbf{x}$ nello spazio Euclideo $D$-dimensionale (nel nostro caso $D=2$).
Goal: Partizionare le osservazioni in un certo numero $K$ di clusters i quali hanno come centroidi il punto $\mathbf{\mu}_{k}$.
- $\mathbf{\mu}_{k}$ → Il centro del cluster (prototipo del cluster)
- $\mathbf{x}_{n}$ → Data point
- $r_{nk}$ → Variabili indicatrici, se il dato $\mathbf{x}_{n}$ appartiene al cluster $k$ allora $r_{nk} = 1$, altrimenti $0$.
Quello che ci resta da fare è $\min{J}$ (a volte viene chiamata distortion oppure inertia).
Iterazioni in dettaglio¶
L'algoritmo K Means è un metodo iterativo di Expectation-Maximization (EM) ed è definito come segue:
- Generiamo i $\mathbf{\mu}_{k}$ centroidi dei cluster randomicamente.
Assegnamo il punto $\mathbf{x}_{n}$ al cluster centroide ${k}$ più vicino settando $r_{kn}=1 $ se $k=\text{argmin}_{j} \parallel \mathbf{x}_{n} - \mathbf{\mu}_{j} \parallel$
Ricomputiamo i centroidi $\mathbf{\mu}_{k}$ in modo da minimizzare $J$. Ossia facciamo la media dei punti. $\mathbf{\mu}_{k} = \frac{\sum_{n} r_{nk} \mathbf{x}_{n}}{\sum{n}r_{nk}}$
Ripetere fino a convergenza

Esempio¶
# Sci-kit learn per la creazione di dati sintetici
from sklearn.datasets.samples_generator import make_blobs
# Librerie per visualizzazioni di dati
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
# Creiamo i dati sintetici
X, y_true = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)
plt.scatter(X[:, 0], X[:, 1], s=50, alpha=0.6)
from sklearn.cluster import KMeans
# Inizializziamo la classe KMeans e fittiamo i dati
kmeans = KMeans(n_clusters=4)
kmeans.fit(X)
# Printiamo le predizioni
y_kmeans = kmeans.predict(X)
print(y_kmeans)
# Visualizziamo le predizioni e coloriamo i punti di conseguenza
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis', alpha=0.6)
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.8, marker='+')
Osservazioni¶
- Efficiente $O(ntk)$ ✔️
- Assunzione sul numero di clusters (dobbiamo sapere $k$ a priori) ❌❌
- Garanzia di convergenza, ma non al minimo globale (posso convergere ad una partizione poco significativa) 😕
- Non robusto con dati rumorosi (gli outliers influiscono molto nella partizione) ❌
- K Means funziona bene quando i cluster sono sferici e con la stessa densità ✔️
DBSCAN: Density-Based Clustering Based on Connected Regions with High Density¶
Algoritmo¶
L'algoritmo suddivide i punti in tre tipi:
- Core Points → Identificano punti in regioni "dense"
- Density-reachable Points → Identificano "boundary points" ai confini delle regioni dense
- Noise Points → Identificano punti che non appartengono a nessuna regione densa.
DBSCAN in a nutshell:
- Inizio: tutti i punti sono settati a unvisited
- Per ogni punto $p$ settato a unvisited
- Setta $p$ come visited
- if $|N_\epsilon(p)| < minPts$
- Setta $p$ come Noise, goto step 2
- note that the noise label might be updated later
- Crea un nuovo cluster $C = \{p\}$
- Crea una coda $Q=N_\epsilon(p)$
- Per ogni $q$ in $Q$:
- if $q$ is unvisited
- Setta $q$ come visited
- if $|N_\epsilon(q)|\geq minPts$:
- $Q \gets Q \cup N_\epsilon(q)$
- if $q$ non è ancora parte di nessun cluster, aggiungilo a $C$
- if $q$ is unvisited
Iterazioni in dettaglio¶
Esempio¶
# Sci-kit learn per la creazione di dati sintetici
from sklearn.datasets.samples_generator import make_blobs
# Creiamo i dati sintetici
X, y_true = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)
plt.scatter(X[:, 0], X[:, 1], s=50, alpha=0.6)
from sklearn.cluster import DBSCAN
# Inizializziamo la classe KMeans e fittiamo i dati
dbscan = DBSCAN(eps=0.7, min_samples=10)
dbscan.fit(X)
# Printiamo le predizioni
print(dbscan.labels_)
# Visualizziamo le predizioni e coloriamo i punti di conseguenza
plt.scatter(X[:, 0], X[:, 1], c=dbscan.labels_, s=50, cmap='viridis', alpha=0.6)
Osservazioni¶
- Genera cluster di forma arbitraria ✔️ ✔️
- Ottimo a gestire il Noise (outliers) ✔️ ✔️
- Efficiente $O(nlogn)$ ✔️
- Incapace di distinguere clusters con densità diverse ❌
- Parametri da settare PAINFUL! ❌❌
Hands on Lab! 👨💻¶
Challenge: KMeans vs DBSCAN¶
In questa challenge vi viene chiesto semplicemente di giocare con i parametri degli algoritmi e di capire come si comportano nei diversi scenari.
Quali sono i pro ed i contro d'utilizzo?
Blob di dimensione diversa¶
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
from sklearn.cluster import DBSCAN
n_samples = 1500
random_state = 170
X, y = make_blobs(n_samples=n_samples, random_state=random_state)
X_filtered = np.vstack((X[y == 0][:500], X[y == 1][:100], X[y == 2][:10]))
# -----------------Modificare i parametri degli algoritmi-----------------------
# Kmeans
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_filtered)
# DBSCAN
y_pred2 = DBSCAN(eps=1.5, min_samples=3).fit_predict(X_filtered)
# ------------------------------------------------------------------------------
# Plot
fig, (ax1,ax2) = plt.subplots(1,2,figsize=(15,5))
ax1.scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred, alpha=0.6, s=50, cmap='viridis')
ax1.set_title("Kmeans : Blob dimensione diversa")
ax2.scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred2, alpha=0.6, s=50, cmap='viridis')
ax2.set_title("DBSCAN : Blob dimensione diversa")
plt.show()
print(y_pred2)
Blob con varianza diversa¶
n_samples = 1500
random_state = 170
X, y = make_blobs(n_samples=n_samples, random_state=random_state)
X_varied, y_varied = make_blobs(n_samples=n_samples,
cluster_std=[1.0, 2.5, 0.5],
random_state=random_state)
# -----------------Modificare i parametri degli algoritmi-----------------------
# Kmeans
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_varied)
# DBSCAN
y_pred2 = DBSCAN(eps=0.6, min_samples=10).fit_predict(X_varied)
# ------------------------------------------------------------------------------
# Plot data
fig, (ax1,ax2) = plt.subplots(1,2,figsize=(15,5))
ax1.scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred, alpha=0.6, s=50, cmap='viridis')
ax1.set_title("Kmeans : Varianza diversa")
ax2.scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred2, alpha=0.6, s=50, cmap='viridis')
ax2.set_title("DBSCAN : Varianza diversa")
plt.show()
Blob con distribuzione anisotropica¶
n_samples = 1500
random_state = 170
X, y = make_blobs(n_samples=n_samples, random_state=random_state)
transformation = [[0.60834549, -0.63667341], [-0.40887718, 0.85253229]]
X_aniso = np.dot(X, transformation)
# -----------------Modificare i parametri degli algoritmi-----------------------
# Kmeans
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_aniso)
# DBSCAN
y_pred2 = DBSCAN(eps=0.3, min_samples=10).fit_predict(X_aniso)
# ------------------------------------------------------------------------------
# Plot data
fig, (ax1,ax2) = plt.subplots(1,2,figsize=(15,5))
ax1.scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred, alpha=0.6, s=50, cmap='viridis')
ax1.set_title("Kmeans : Blob con distribuzione anisotropica")
ax2.scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred2, alpha=0.6, s=50, cmap='viridis')
ax2.set_title("DBSCAN : Blob con distribuzione anisotropica")
plt.show()
Challenge: Digits Dataset¶
Applicare KMeans al dataset Digits e visualizzare i centroidi trovati
Plot dei primi 10 esempi e dei relativi centroidi ai quali sono stati assegnati
Visualizzare come cambiano le imamgini relative ai centroidi per ogni iterazione dell'algoritmo (10 iterazioni) e plottare la relativa distorsione. Per la riproducibilità dell' esercizio inizializzare l'algoritmo con i seguenti parametri:
KMeans(n_clusters=10, max_iter=???, n_init=1, init='random', random_state=1337)
Hints:
- Le immagini sono 8x8 (usare
.reshape()per visualizzarle) - Il numero di classi 10
from sklearn.datasets import load_digits
# Load del dataset
digits = load_digits()
digits.data.shape
# Visualizzazione del primo elemento
ax = plt.axes(xticks=[], yticks=[])
ax.imshow(digits.data[0,:].reshape(8,8), cmap="Greys")
# Run kmeans!
kmeans = KMeans(n_clusters=10)
kmeans.fit(digits.data)
# Visualizziamo i centroidi trovati
fig, axs = plt.subplots(1,10, figsize=(10,10))
for i in range(10):
axs[i].imshow(kmeans.cluster_centers_[i].reshape((8,8)), cmap="Greys")
axs[i].set_xticks([])
axs[i].set_yticks([])
fig, axs = plt.subplots(2,10, figsize=(10,3))
# Plot dei primi 10 esempi e dei relativi centroidi ai quali sono stati assegnati
for i in range(10):
axs[0,i].imshow(kmeans.cluster_centers_[kmeans.labels_[i]].reshape((8,8)), cmap="Greys")
axs[1,i].imshow(digits.data[i,:].reshape((8,8)), cmap="Greys")
axs[0,i].set_title("Predict")
axs[1,i].set_title("True")
axs[0,i].set_xticks([])
axs[1,i].set_xticks([])
axs[0,i].set_yticks([])
axs[1,i].set_yticks([])
distortion = []
for i in range(10):
max_iter = i+1
# Facciamo andare kmeans con (i+1) iterazioni
k_means = KMeans(n_clusters=10, max_iter=max_iter, n_init=1, init='random', random_state=1337)
k_means.fit(digits.data)
# Print della distorsione (intertial_ su scikit)
print (f"Iterazione: {max_iter} | Distorsion = {k_means.inertia_}")
distortion.append(k_means.inertia_)
# Visualizzazione dei centroidi ad ogni iterazione
fig, axs = plt.subplots(1,10, figsize=(10,2))
for j, ax in enumerate(axs.flatten()):
ax.imshow(k_means.cluster_centers_[j].reshape((8,8)), cmap="Greys")
ax.set_xticks([])
ax.set_yticks([])
plt.show()
# Plot della distorsione
plt.plot(distortion, 'o', linestyle='-')
plt.xticks([x for x in range(10)])
plt.ylabel("Distorsion")
plt.xlabel("Iterazione")
plt.grid()
Valutazione del clustering¶
Come facciamo a sapere se il nostro algoritmo ha dato dei buoni risultati o meno? Servono delle metriche che studino la bontà di un clustering.
...ma...
Qual è il problema principale della valutazione in ambito unsupervised?

NON ABBIAMO IL GROUND TRUTH!
Nel caso in cui non abbiamo nessun tipo di etichetta si utilizzano valutazioni intriseche come ad esempio il Silhouette coefficient.
Nel caso, però, in cui abbiamo le etichette disponibili possiamo fare delle valutazioni estrinseche: ARI, AUROC, F-Score ecc. Nel caso del Digit Dataset abbiamo le etichette disponibili possiamo dunque plottarci l'accuracy e la confusion matrix.
from scipy.stats import mode
import numpy as np
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
# Run kmeans!
k_means = KMeans(n_clusters=10)
k_means.fit(digits.data)
# Perchè questo passaggio??? :)
labels = np.zeros_like(k_means.labels_)
for i in range(10):
mask = (k_means.labels_ == i)
labels[mask] = mode(digits.target[mask])[0]
accuracy = accuracy_score(digits.target, labels)
print(f"Accuracy : {accuracy}")
# Confusion Matrix
mat = confusion_matrix(digits.target, labels)
sns.heatmap(mat.T, square=True, annot=True, fmt='d', cbar=False,
xticklabels=digits.target_names,
yticklabels=digits.target_names)
plt.xlabel('Label True')
plt.ylabel('Predicted Label ')
plt.show()
# Possiamo clcolare l'accuracy anche così
mat.trace()/mat.sum()
Challenge: Quantizzazione Immagine¶
Un'immagine è formata da pixels. Ogni pixel è identifica un colore. Ogni colore è identificato da una tripletta RGB che corrispondono ai canali Red Green Blue. Normalmente i canali RGB sono su 8bit ciascuno e di conseguenza codificano $2^{8}$ intensità ciascuno.
- Quante combinazioni di colori possiamo avere in totale?
r g b
[0..255][0..255][0..255]Riusciamo a quantizzare un'immagine comprimendola solo su 16 colori?
- Usare KMeans per comprimere l'immagine su 16 colori.
from sklearn.datasets import load_sample_image
# Show dell'immagine
china = load_sample_image("china.jpg")
ax = plt.axes(xticks=[], yticks=[])
ax.imshow(china)
china.shape
# Scaliamo i dati da 0..1
data = china / 255.0
data = data.reshape(427 * 640, 3)
data.shape
from sklearn.cluster import KMeans
# Embeddiamo i colori su 16 dimensioni
kmeans = KMeans(n_clusters=16)
kmeans.fit(data)
# Visualizzazione dei centroidi
cmap = sns.palplot(kmeans.cluster_centers_)
# Show immagine quantizzata
ax = plt.axes(xticks=[], yticks=[])
ax.imshow(kmeans.cluster_centers_[kmeans.predict(data)].reshape(china.shape))
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.colors import ListedColormap
# Creazione della colormap utile
cmap = ListedColormap(kmeans.cluster_centers_)
# Show clusters nello spazio (normalizzato) RGB
sp = plt.figure().add_subplot(111, projection='3d')
sp.set_xlabel('R')
sp.set_ylabel('G')
sp.set_zlabel('B')
sp.scatter(data[:,0], data[:,1], data[:,2], s=1, c=kmeans.labels_, cmap=cmap)
# Installiamo il modulo direttamente dalla cella con il comando magico !pip install
!pip install hdbscan
import hdbscan
# Tocca a te! Enjoy!